Force Field Methods

Contents

In force field or molecular mechanics methods such as (classical) MD, the potential energy surface is calculated as independent of the nuclear coordinates.

In an MD simulation, the energy is calculated using an empirical force field, which has been fitted to experimental data. In the case of ab initio force fields the energy is fitted to high level computational data.

In force field methods bonds are often treated harmonically, i.e. using a ball on a spring model. The movement of the electrons is assumed to be a function of the nuclear motion (Born-Oppenheimer approximation). Since solving the electronic Schrödinger equation is bypassed using force field methods, the bonding information must be given explicitly.

Molecular mechanics methods work because of the observation that different groups behave similarly regardless of the molecule they are part of.

The force field energy is given as a sum of terms, each term being the energy required to distort the molecule in a specific fashion.

E_{F F} = E_{s t r} + E_{b e n d} + E_{t o r s} + E_{v d w} + E_{e l} + E_{c r o s s}

where $E_{s t r}$ is the energy required to stretch a bond between two atoms, $E_{b e n d}$ is the energy required to bend an angle, $E_{t o r s}$ is the torsional energy of rotation around a bond. $E_{v d w}$ and $E_{e l}$ are non-bonded interactions and describe the van der Waals and electrostatic energy respectively. $E_{c r o s s}$ describes the coupling between the bonded interactions.

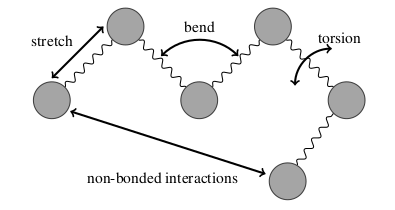
Force Field Terms.png

The combination of these energy terms allows for the construction of the Potential Energy Surface which effectively gives the energy of a molecule as a function of its geometry.

Bond Stretching Energy
Bond Bending Energy
Bond Torsion Energy
van der Waals Energy
Electrostatic Energy
Non-Bonded Coupling Energy

The combination of these energy terms allows for the construction of the Potential Energy Surface which effectively gives the energy of a molecule as a function of its geometry for example, the CHARMM force field ^[1] ^[2] ^[3]

Bond Stretching Energy

$E_{s t r}$ is the energy required to stretch or compress a bond from its “natural” or equilibrium bond length. The simplest method of calculating bond stretch energy is a Taylor expansion around a “natural” bond length that is terminated at the second order, giving a harmonic approximation.

E (r) = \frac{1}{2} k (r - r_{0})^{2}

where $r_{0}$ is the natural or equilibrium bond length, $r$ is the distance between the atoms and $k$ is the force constant.

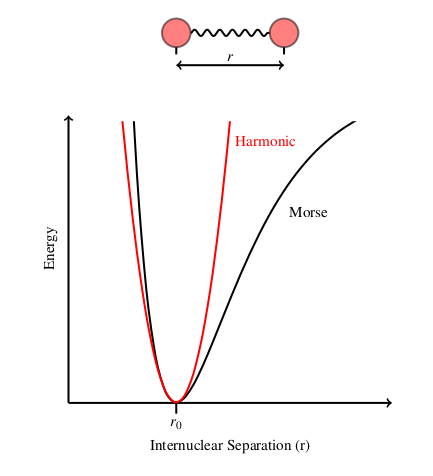
The accuracy of this harmonic approach can be increased by using higher order terms but this has the disadvantage of being more computationally expensive. The harmonic potential is quite accurate close to the equilibrium bond length but increasingly inaccurate further away from this point. Hence it is sometimes more appropriate to use the Morse potential to calculate the bond stretch energy.

E (r) = D_{e} (1 - e^{- α (r - r_{0})})^{2}

α = \sqrt{\frac{k_{e}}{2 D_{e}}}

where $D_{e}$ is the well depth, $r$ is the distance between the atoms and $r_{0}$ is the equilibrium bond length. $α$ is related to $k_{e}$ which is the force constant at the minimum of the potential well.

The Morse potential is more accurate than the harmonic potential but it is not without its limitations. For long bond lengths the restoring force is small, which results in distorted structures displaying slow convergence towards equilibrium bond length.

The Morse potential is compared to the harmonic potential below.

Harmonic and Morse Potential.png

Bond bending energy

$E_{b e n d}$ is the energy required for bending an angle formed by three atoms
A-B-C in which A and B and B and C share a bond. Like $E_{s t r}$ , $E_{b e n d}$ can be
found using a harmonic approximation.

$E (θ) = \frac{1}{2} k (θ - θ_{0})^{2}$

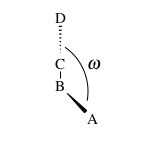
Bond torsion energy

$E_{t o r s}$ is the energy change associated with the rotation around a B-C bond in a
four atom sequence A-B-C-D where A is bonded to B, B to C and C to D. If one
looks down the length of the B-C bond then a torsional angle is defined as the
angle (ω $ω$ between the A-B and the C-D bonds as shown. The angle $ω$ is often expressed as a range from -180◦ to 180◦ , encompassing a full rotation of the bond.

torsion angle.png

The torsion energy differs from the stretch and bend energies in a number of ways. The energetic penalty for distorting a molecule away from minimum structure is quite low for bond rotations, meaning that large deviations from the minimum energy structure may occur. The barrier for bond rotations has contributions from non-bonded interactions e.g. van der Waals, hence the torsion energy is also coupled to the non-bonded parameters. The torsion energy must also be periodic i.e. if a bond is rotated 360◦ the energy will return to the same value. Because of this periodicity, Etors is often expressed as a Fourier series:

$E_{t o r s} (ω) = \sum_{(n = 1)} V_{n} \cos (n ω)$

where $V_{n}$ determines the size of the rotational barrier around B-C. The $n = 1$
term describes a rotation about a bond that is periodic by 360◦ , $n = 2$ a rotation
that is periodic by 180◦ , $n = 3$ by 120◦ etc. $n$ controls the number of minima in
the rotational energy.

Van der Waals Energy

The van der Waals term includes the energy between two permanent dipoles, the force between an induced dipole and a permanent dipole and the interaction between two induced dipoles. $E_{v d w}$ describes the repulsion or attractions between atoms that are not directly bonded and not due to the electrostatics. $E_{e l}$ describes the energy of interaction between fixed partial charges within the molecule. $E_{v d w}$ is zero for large inter-atomic distances, rapidly becoming very repulsive for short distances. This repulsion can be attributed to the overlap of the electron clouds of the two atoms which occurs at short internuclear distances. The van der Waals interaction is very slightly attractive at intermediate distances due to induced dipole-dipole interactions. A popular method for incorporating the van der Waals energy is by means
of a Lennard-Jones potential which can be given as:

$E_{L J} (R) = ϵ [{(\frac{R_{0}}{R})}^{12} - 2 {(\frac{R_{0}}{R})}^{6}]$

where $R_{0}$ is the minimum energy distance, $R$ is the internuclear separation and $ϵ$ is the depth of the minimum.

Electrostatic Energy

The electrostatic energy of the force field is given by the Coulomb potential:

$E_{e l} (r_{i j}) = \frac{Q_{i} Q_{j}}{ϵ r_{i j}}$

where $ϵ$ is a dielectric constant, $Q$ is the charge of atom A or B and $R_{A B}$ is the distance between them. The Coulomb potential can be expanded to take into account dipoles, multipoles and polarizabilities.

Non-Bonded Coupling Energy

The final term in the force field energy is a cross term that takes into
account the coupling between the other, fundamental terms. These cross terms are usually written as a Taylor expansion of the individual coordinates, but are not present in every force field. There are a number of packages available for carrying out MD simulations including, but not limited to, CHARMM,^[4] ^[1:1]
NAMD ^[5] and GROMACS ^[6] ^[7] and many of these have their own forcefield, for example, in the case of the CHARMM forcefield^[2:1] ^[3:1] and the GROMOS forcefield.^[8]

B. R. Brooks, III Brooks, C. L., Jr. Mackerell, A. D., L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York, and M. Karplus. CHARMM: The biomolecular simulation program. J. Comput. Chem., 30:1545–1614, 2009. ↩︎ ↩︎
A. D. MacKerell, D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin, and M. Karplus. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B, 102:3586–3616, 1998. ↩︎ ↩︎
A. D. Mackerell, M. Feig, and C. L. Brooks. Extending the treatment of backbone energetics in protein force fields: Limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. J. Comput. Chem., 25:1400–1415, 2004. ↩︎ ↩︎
B. R. Brooks, R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan, and M. Karplus. CHARMM - a program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem., 4:187–217, 1983. ↩︎
J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale, and K. Schulten. Scalable molecular dynamics with NAMD. J. Comput. Chem., 26:1781–1802, 2005 ↩︎
B. Hess, C. Kutzner, D. van der Spoel, and E. Lindahl. GROMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput., 4:435–447, 2008. ↩︎
S. Pronk, S. Pall, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M.R. Shirts, J.C. Smith, P.M. Kasson, D. van der Spoel, B. Hess, and E. Lindahl. GROMACS 4.5: a high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics, 29:845–854, 2013. ↩︎
C. Oostenbrink, A. Villa, A. E. Mark, and W. F. Van Gunsteren. A biomolecular force field based on the free enthalpy of hydration and solvation: The GROMOS force-field parameter sets 53A5 and 53A6. J. Comput. Chem., 25:1656–1676, 2004. ↩︎